Calculus
Real analysis
Measure and integral calculus
Historical development
The calculus period
This period extended from about 1670 to the beginning of the 19th century, beginning with the creation of the calculus by Leibniz and Newton.
Newton, influenced by his teacher Barrow and his preoccupation with dynamics—dealing with forces and their relation, primarily to motion—used a universal independent variable conceived primarily as time; thus, he had no concept of functions of several variables and hence none of partial derivatives. The primary concept was that of fluxion (derivative) and arose from kinematic considerations. The concept of integral was not isolated, and no symbol for integration was introduced. His first basic problem was to find fluxions. Integration was treated in a geometric form as a search for fluents (antiderivatives, primitives, indefinite integrals), functions the fluxions of which are given.
Newton depended mainly on the fact that the derivative of a variable area F(x) under a curve is the ordinate f(x) of this curve. For Newton, moreover, integration was only a particular case of his second basic problem: given an equality containing fluxions, find the corresponding relation for fluents (solve ordinary differential equations). He solved this problem formally by means of series.
Leibniz, influenced by Pascal, conceived the derivative as the slope of a tangent and the integral as summa omnium linae (“the sum of all lines?). The main purpose of his activity was to devise a universal language—that is, a general formalism for the acquisition and organization of knowledge. He largely succeeded in the creation of such a formalism for the calculus, and the present formalism is still essentially and properly his, including the integral symbol (a stylized form of the letter S standing for summa omnium). His also are the terms constant, variable, parameter, and (with the help of the Swiss mathematician Johann Bernoulli) function and integral.
The heroic years of the calculus at the end of the 17th century saw the constant flow of new results from Leibniz and his school, as embodied in the work of Jakob Bernoulli, Johann Bernoulli, and G.F.A. de l'Hospital. During the 18th century, the Scottish mathematician Colin Maclaurin pursued and developed Newton's ideas and attempted to clarify them in his Treatise of Fluxions (1742), while the Swiss mathematician Leonhard Euler pursued further the ideas of Leibniz and his school in his Introductio in Analysin Infinitorum of 1748 and attempted to found the calculus upon an obscure passage to the limit, starting with the calculus of differences.
Mathematicians of the 18th century devoted little effort to the shaky foundations of the calculus, apparently happy with the powerful tools at their disposal, the fecundity of the methods, the beauty and consistency of the results. Discussions about the metaphysics of calculus were left to philosophers and theologians, among whom the Irish-born Anglican Bishop George Berkeley figured prominently. The whole subject of metaphysics of calculus vanished into thin air, however, with the French mathematician Jean Le Rond d'Alembert's two articles on “Limite? and “Différentielle? in the Encyclopédie (1751–65). At last the concept of limit was isolated, a concept that had run as an almost invisible thread in the fabric of infinitesimals as woven since Stevin and others at the turn of the 17th century. The concept of differentiation, too, was finally defined rigorously in terms of limits. (Yet, after d'Alembert, Lagrange still tried to define integration in terms of Newton's conception of a function as a power series.)
The analysis period
A new era opened in France with Augustin-Louis Cauchy's Résumé des leçons sur le calcul infinitésimal (1823), the basis of which was the concept of limit. Differentiation was defined by a passage to the limit. At last, the integral was defined directly and in purely analytic terms by returning to the very essence of the method of exhaustion as follows: Given a bounded function f(x) defined for a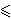 
x 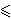b the interval [ a, b } may be divided into n subintervals by means of points a = xo < x1 < ...< xn = b, and the Eudoxus-Archimedes-Cauchy sums (see 20; nowadays called Riemann sums) may be formed by adding n terms, each composed of a product of a value of f and the length of a subinterval, with f evaluated at an intermediate point of the subinterval. The limit of these sums, as the largest length of the subintervals converges to zero, is, by definition, the integral of the function f on [ a, b ], provided that this limit exists and is independent of the choice of the t k, the intermediate point in the subinterval at which f is evaluated.
A new way of thinking was thus born; existence of integrals as well as of derivatives was no longer a question of faith but a problem to be studied. Cauchy gave an incomplete proof of the existence of integrals of continuous functions, a proof that was completed only in 1875 by the French mathematician Gaston Darboux. Meanwhile, Riemann in 1854 (published in 1867) gave necessary and sufficient conditions for the existence of the integral called the Riemann integral and showed that continuous and piecewise monotone functions satisfy these conditions. Instead of Riemann sums, Darboux introduced the upper and lower Darboux sums, replacing the value of f at an intermediate point in an interval by M k and m k', which, respectively, denote the least upper and the greatest lower bounds of f(x), as x varies between x k and x k + 1. The passage to the limit yields the upper and lower Darboux integrals. These two integrals coincide if and only if the bounded function f is Riemann-integrable on [ a, b ].
Copyright © 1994-2002 Encyclopædia Britannica, Inc.
Sources
- Encylopedia Britannica 2002, Expanded Edition DVD